| 前頁 | 目次 | 次頁 | ||||||||||||||||||||||||
|
沸騰水型原子炉の炉心熱設計手法及び 昭和51年2月16日
原子炉安全専門審査会
標記について、当審査会の炉心熱設計検討会は別添の報告をまとめた。この内容は妥当と考えられるので、今後当審査会の安全審査の段階では次に掲げる点に留意してGEXL相関式及びGETABの考え方を用いることとする。 1 GEXL相関式の適用は、7×7型及び8×8型格子配列の燃料集合体に限られることは当然のことながら種々の燃料集合体構成要素の形状及び寸法の相違に留意すること。 2 GEXL相関式の適用にあたって、8×8型燃料集合体の算出標準偏差の2.8%は、そのデータベースが7×7型燃料集合体のデータベースとは同様でないことを考慮して、7×7型燃料集合体についての算出標準偏差の3.6%と暫定的に同じ値にすること。 3 GETABに用いるプラントの各パラメータの標準偏差決定のために、今後国内においても各種データの集積を行うこと。 4 GETABの考え方は、局所的な過渡状態についても適用すること。 5 運転制限値決定に際しては低出力状態例えば高温待機状態からの過渡状態は検討対象から除外して差し支えないが、そのような過渡状態においても炉心全燃料棒数の99.9%以上が沸騰遷移を生じないことを確認すること。 (別添)
沸騰水型原子炉の炉心熱設計手法及び熱的運転制限値決定手法について
昭和51年2月16日
原子炉安全専門審査会
炉心熱設計検討会
Ⅰ 検討範囲
本検討は、GE社が開発した沸騰遷移相関式GEXL(GE Critical Quality(Xc)-Boiling Length (LB)Correlation)及びGEXLに基づく熱設計手法GETAB(GE Thermal Analysis Basis)について、GE社の文献(1)(2)及び検討に際しての質問への回答(3)を骨子として行ったものである。 Ⅱ 沸騰遷移相関式
この報告書の中で用いられている「沸騰遷移」(Boiling Transition)という用語は、核沸騰を越えた状態の開始という意味である。 1.Hench-Levy相関式
GE社の沸騰水型炉においては、これまで沸騰遷移を判断する手法として限界熱流束比CHFR(Critical Heat Flux Ratio)という考え方を用いてきた。CHFRは限界熱流束--すなわち、燃料集合体のある点において沸騰遷移を生じさせる熱流束--と実際の熱流束との比として定義され、熱的余裕を示す指標となっている。 限界熱流束の計算には、J.E.Hench及びS.Levyらによって開発され、1966年に発表されたHench-Levy相関式を用いており、この式の一般的な形は次のようになっている。 φc=f(G,P,X)
φc:局所限界熱流束
G:冷却材質量流量
P:冷却材圧力
X:断面平均クオリティ
このHench-Levy相関式のデータベースは、4本及び9本の模擬燃料棒で構成された集合体での約780点の実験データであり、GEはHench-Levy相関式はこれらのデータの下限線と考えていた。 2.GEXL相関式
2-1 GEXL相関式
Hench-Levy相関式に代る新しい沸騰遷移の開始を判断する式として提案されているGEXL相関式は、出力分布依存性を除去する手段として限界クオリティ対沸騰長さの関係を導入してデータを整理し、ベストフィットとして得られた式である。この式を用いて沸騰遷移を判断する手法としてはCHFRに代って限界出力比CPR(Critical Power Ratio)の考え方を用いる。CPRは限界出力-すなわち、燃料集合体のある点において沸騰遷移を生じさせる燃料集合体出力-と実際の燃料集合体出力との比として定義され、熱的余裕を示す指標となっている。 GEXL相関式は一般的な形として次のようになっている。 Xc=f(LB,DQ,G,L,P,R)
Xc:断面平均限界クオリティ
LB:沸騰長さ
DQ:熱的等価直径
G:冷却材質量流量
L:加熱長さ
P:冷却材圧力
R:局所ピーキングパターンに関する係数
GEXLを用いた限界出力の計算は、次に述べる手法によって行う。 1)着目する燃料集合体の冷却材の質量流量、圧力、入口エンタルピ等を用いてGEXL相関式によって限界クオリティ対沸騰長さを計算する。 2)着目する燃料集合体の出力分布を固定させたうえで出力を変化させクオリティ対沸騰長さを求め、1)で得た限界クオリティ対沸騰長さの曲線にある点で接するような出力を限界出力とする。 この関係を第1図(1)に示す。 2-2 データベース
GEXL相関式は、7×7型及び8×8型燃料集合体を模擬した16本、49本及び64本の加熱模擬集合体を用いコロンビア大学のループ及びGEのATLASループで得られた定常実験データに基づいており、そのデータは第1表に示す1703点である。 上記のデータから作成されたGEXL相関式は、7×7型燃料集合体については2,700点、8×8型燃料集合体については1,298点の定常実験データでの検証が行われた。以上、相関式の基礎データならびに検証用データを得た際の実験パラメータ範囲は次のとおりである。 冷却材圧力:800~1,400psia(56.2~98.4㎏/㎝2)
質量流量:0.10×106~1.25×106lb/hr-ft2(0.49×106~6.10×106㎏/hr-㎡)
入口サブクーリング:0~100Btu/lb(0~55.6Kcal/㎏)
局所ピーキング:コーナ1.61□内側1.47
軸方向出力形状:一様、コサイン、入口ピーク、出口ピーク、ダブルハンプ
第1表 相関式作成に用いられたデータ数 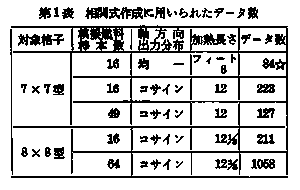 ☆ コロンビア大学データ
これらのデータとGEXL相関式を用いた予測値との対照例を第2図から第4図(1)にまで示す。GEXL相関式による予測値と実測値との比の標準偏差σは、第5図及び第6図に示すように7×7型燃料集合体においては3.6%、8×8型燃料集合体においては2.8%となる。 また、定常実験データとの検証と同様に流量、出力及び圧力を変化させた非定常実験データとの比較も行われている。 Ⅲ GETAB
従来、GEの沸騰水型炉の熱設計及び運転士の熱的制限条件は、運転員の単一誤操作あるいは機器の単一故障に起因する過渡状態においてもCHFRが1.0以下にならないようにするという考え方に基づいていた。CHFRが1.0以下にならなければよいというのは、CHFを算出するHench-Levy相関式が実験データの下限線に対応するものであるという考え方から正当化される。実際には定格出力においてCHFRが1.9以上であるように設計及び運転を行うことになっており、このように余裕を持たせておけば、種々の過渡状態においてもCHFRが1.0以上に留ることが示されていた。 今回、GEが提案している新しい熱設計手法GETABは、次のような考え方を骨子とするものである。 1)熱的余裕を評価する新しい指標として、GEXL相関式に基づくCPRを用いる。 2)GEXL相関式による沸騰遷移の予測、プラント運転条件、燃料製造公差、計測器等の不確定性を統計的に取り扱い、この変動を見込んだ定格出力においても、炉心全燃料のうち沸騰遷移を起こさないものが確率的にある値以上確保されるように最小限界出力比MCPRを定める。 3)次に各種の過渡状態の解析を行ってそれぞれのCPRの減少分ΔCPRを求め最も大きい減少分を2)で得られたMCPRに加えて定常状態での熱的運転制限条件とする。 4)上記2)にいうある値は、99.9%とする。 Ⅳ GEXL相関式及びGETABの適用についての見解
1.GEXL相関式について
1-1 限界クオリティ対沸騰長さ型相関式についてこの型の沸騰遷移相関式は特に新しいものではなく、Hewitt(4)あるいはCISE(5)が既に開発した相関式と同じ考え方である。CISEの研究結果によれば、この型の相関式は沸騰遷移の予測が出力分布ほとんど左右されないという長所を持っている。Westinghouse社が用いているW-3相関式でも熱流束修正係数について最大のメモリ効果を仮定した場合、この考え方と同一となる。 Hench-Levy相関式との比較において、GEXL相関式の長所は、GEXL相関式が実形状模擬の集合体データから得られたものであり、軸方向出力分布形状及び局所ピーキング係数が考慮されていることである。従って、限界クオリティ対沸騰長さの関係にデータを整理して得られたGEXL相関式は、種々の出力分布形状に対しての予測能力の不確定性が非常に減少しており、種々の原子炉運転状態に対して沸騰遷移を適確に判断するのに好都合である。 1-2 データベースとの関連について
GEXL相関式は、実際に原子炉に用いる格子形状等の模擬集合体の実験から得られているのが長所ではあるが、その適用に当たっては7×7型及び8×8型格子配列の燃料集合体に限られることは当然のことながら種々の燃料集合体構成要素の形状及び寸法の相違に留意すべきである。 GEXL相関式の予測能力の実験データとの検証において算出された標準偏差は、後述のモンテカルロ計算に用いられるが、8×8型燃料集合体についての算出標準偏差の2.8%はそのデータベースが7×7型燃料集合体のデータベースと同様ではないことを考慮して7×7型燃料集合体についての算出標準偏差の3.6%と暫定的に同じ値にすべきである。 また、GEXL相関式を過渡現象解析において用いたことは、定常実験のデータは沸騰水型炉心内の過渡状態に対して概して安全側の評価を与えるとの理解及び非定常実験の結果(1)に基づき妥当である。 2.GETABについて
2-1 確率論的な考え方について
前述したように、GETABの特徴は、GEXL相関式に基づくこと及び確率論的な考え方を採用したことである。GEXL相関式の評価については前述のとおりであり、ここでは確率論的な考え方についての見解を示す。 従来沸騰水型炉の設計に用いられてきたHench-Levy相関式は、実験で観測されたCHFの下限線であるとされている。これは、この相関式が開発された当時までの観測値の下限であって、この下限線は沸騰遷移が生ずる確率が十分に少ないことを示す線と解することができる。また加圧水型炉に用いられている沸騰遷移相関式についても同様なことが言えるのであって例えばW-3相関式による最小DNBRが1.3であることは95%の信頼度で沸騰遷移を起こさない確率が95%以上であることを意味するとされている(6)。GEXL相関式は、その基礎となるデータが質及び量共に有意の統計処理を可能とする程度に充実していると考えられるので、この相関式を確率論的な立場から評価検討するのは、より厳密な態度であると判断する。GETABにおいては、CPRが1.05の場合には、その燃料集合体において95%の信頼度で沸騰遷移を起こさない確率が95%であることに相当することも示されている。 GETABの特色は、確率論的な考え方を単に沸騰遷移相関式のみならず原子炉の運転条件にまで適用し、全炉心において核沸騰を維持している確率を求め、この確率をある値以上にするように運転状態を制限しようとする点にある。この点については、運転条件に影響を与える種々のパラメータについて統計処理に耐えうるデータが存在しているならば、より厳密に炉心の熱的余裕を評価したことになり、また既に確率論的な評価検討を行っているGEXL相関式を適用するのにより首尾一貫した手法であると判断する。従って問題は、統計処理の方法とそれに用いるデータならびに判定の基準の妥当性となる。 GETABは、まずある基準の炉心出力状態から出発し、次に給水流量、温度、圧力、炉心流量、出力分布等の測定誤差や不確かさを正規分布を仮定してモンテカルロ計算を行うことによって考慮し、沸騰遷移を起こす燃料棒数の期待値を求めるものである。この方法は妥当である。 各パラメータの標準偏差は、ほとんどが実績から定められているが各プラント毎に異なる計測器の測定誤差は勿論のこと各種データについて今後国内においても集積を行う必要がある。 基準となる出力状態については、炉心寿命中に予想される出力分布の変化を考慮して多数のケースについて発現確率を定めそれぞれについて上記モンテカルロ計算を行うのが厳密な計算といえる。GETABにおいては、炉心寿命中にほとんど発現する可能性がなく、かつ多くの燃料棒が沸騰遷移を起こすと考えられる出力状態1ケースを解析することとしている。この方法はより厳しい結果を与える方法という意味で容認できるものである。 この様にして求められた沸騰遷移を起こす燃料棒数の期待値について、何本までを許容するかという判定基準としてGETABでは全炉心燃料棒数のうち99.9%以上が沸騰遷移を起こさないという基準が提案されている。この値については、これまで炉心全体にわたって期待値を計算する手法がとられていなかったことから99.9%が従来と比較してどの程度に安全裕度の面で改善されているかは一概にはいえない。しかし以下に述べる点を考慮すればこの99.9%という基準は容認できる。 1)99.9%が沸騰遷移を起こさないとして定めたMCPRの典型的な値たとえば1.05においては95%の確率で熱的に最も厳しい燃料集合体でも沸騰遷移が生じないということに95%の信頼度があることが示されている。このことは、炉心出力状態の変動を考えていない従来の沸騰遷移の考え方、たとえばW-3相関式によるDNBRが1.3以上であることなどと、ほぼ同程度の安全裕度を含んでいるものと判断してもよい。 2)基準出力状態として、前述のように厳しい結果が得られるものを採用しており、99.9%という値にさらに安全余裕が付加されている。 3)仮に沸騰遷移が生じたとしても、それが直ちに燃料焼損につながるものではないことから、99.9%という値は工学的には十分な値である。 2-2 局所現象への適用について
GETABでは、このようにして定ったMCPRの制限値(たとえば1.05)が予想される過渡状態でもおかされることがないように代表的な過渡状態について計算し、これを上記のMCPRの値に加えることとしている。この手法も実用的には容認できるものである。 しかし、炉心の局所的過渡状態については一部の燃料棒がかなり苛酷な状態にさらされてもその数が0.1%以内であれば基準を満足することになり、この意味では従来の方式よりも安全余裕が少なくなる場合もありうる。GEは、炉心全体にわたる過渡状態についてのみΔCPRを考慮することを提案しているが、上述の意味で、局所的な過渡状態についてもΔCPRを考慮すべきである。 2-3 ΔCPRの解析事象について
熱的運転制限値決定のために各原子炉毎に解析すべき過渡状態は、原子炉施設の再循環系、給水系、主蒸気系、制御系等の系統毎に分析し、炉心の熱的条件がそれぞれの系統事象毎に最も厳しくなるものが含まれている必要がある。 なお、低出力状態例えば高温待機状態からの過渡状態については、上記制限値決定に際しての検討対象から除外して差し支えない。ただし、そのような状態においても炉心全燃料棒数の99.9%以上が沸騰遷移を生じないことを確認する必要がある。 3.燃料の熱的健全性について
GEXL相関式及びGETABの適用に当たって、関心を呼ぶのは99.9%以上が沸騰遷移を避けることができるように基準が定められたということであろう。この点について燃料の熱的健全性との関連を特に付記する。 この基準は、あくまでも前述のように炉心熱設計及び熱的運転制限値確立のために必要な数値として選定されたものであり、定った通常運転時のMCPRが例えば1.20であれば全炉心燃料棒数の99.99996%が沸騰遷移を避けられることが解析上示されている。このことは例えば数百万本の燃料棒のうち、1本程度が沸騰遷移を経験することが確率的にありうるということであり、沸騰遷移を経験するものが直ちに燃料被覆管の現実的な破損を意味することではないことを考慮すれば工学的に十分容認できるものである。 また仮にこの基準から定った条件から誘起される燃料被覆管の熱的な面からの破損が0.1%あったとしても、その時の放射性物質の放出量は極く少なく原子炉冷却材浄化系あるいは放射性物質の処理系によって十分処理し得る範囲であり、一般公衆の被曝線量増加の原因とはならないと判断する。 Ⅴ 検討経緯
原子炉安全専門審査会は、沸騰水型炉ならびに加圧水型炉の炉心熱設計手法等の検討のために次のメンバからなる炉心熱設計検討会を昭和50年4月15日の第136回原子炉安全専門審査会において設置した。(敬称略)
炉心熱設計検討会は、沸騰水型炉について各種の文献の調査及びGE、東芝、日立の各原子炉製作会社ならびに東北、東京、中部、中国、日本原子力発電の各電力会社の意見聴取を行って検討した結果、本報告書を作成した。 Ⅵ 引用文献
(1)“General Electric BWR Thermal Analysis Basis(G E T A B)Data,Correlation and Design Application NEDO-10958.GE.Nov.1973.
(2)同上NEDE-10958.GE.Nov.1973
(3)“炉心熱設計検討会質問事項への回答”原子炉規制課編.昭和50年9月26日
(4)“Correlation of Critical Heat Flux for the Vertical Flow of Water in Uniformly Heated Channels”AERE-R5590.G.F.Hewitt etal 1970
(5)“Critical Heat Flux(C H F)Prediction in Complex Geometries(Annuli and Clusters)from a Correlation Developed for Circular Conduits”CISE-R-276.G.P.Gaspari etal.1968
(6)“熱水力設計及び評価”MAPI-1003.三菱原子力工業㈱.昭和49年8月
第1図CPR図式決定法 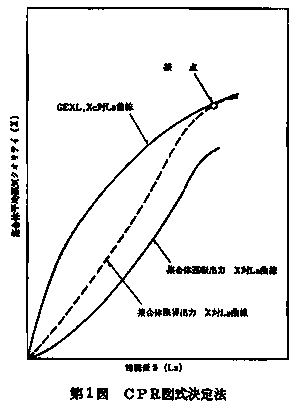 第2図予測対測定限界出力 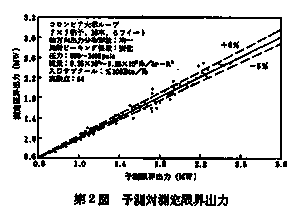 第3図予測対測定限界出力 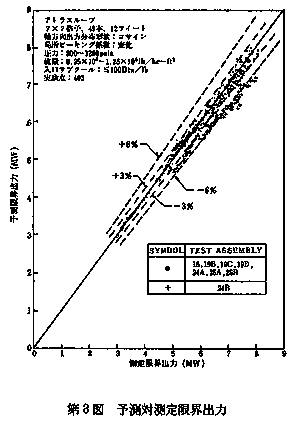 第4図予測対測定限界出力 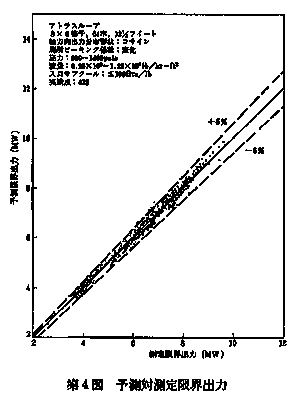 第5図ヒストグラム(頻度対ECPR,7×7格子) 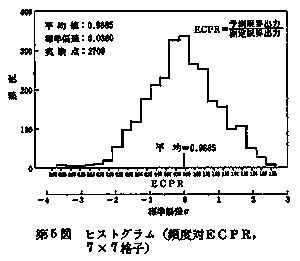 第6図ヒストグラム(頻度対ECPR,8×8格子) 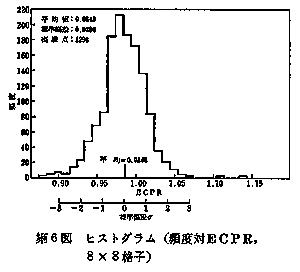 | ||||||||||||||||||||||||
| 前頁 | 目次 | 次頁 |